What is esssential for collision detection?

How accurate do I need to simulate?

Collision detection is essential for realistic physical interactions between material and machine(s), environment (e.g. floor) or other materials in twin.

But the problem is: Simulating a 100% accurate collision is very computationally intensive and should be avoided.

The geometry of some objects is quite complex and leads to a great effort in calculating the impact forces which is not possible in real time. Therefore, there is a mesh simplification or decomposition for this purpose to approximate the object to the real one to reduce the effort.

Note

Before starting simulating my machine, the most important question you need to ask yourself: "How accurate do I NEED to simulate my material?"

Let's look at an example: Simulating pallets.

If the pallets moving on conveyors and need only to get detected by light barriers on the front edge (as shown on the following picture), a box with the same outer dimension would be sufficient enough.

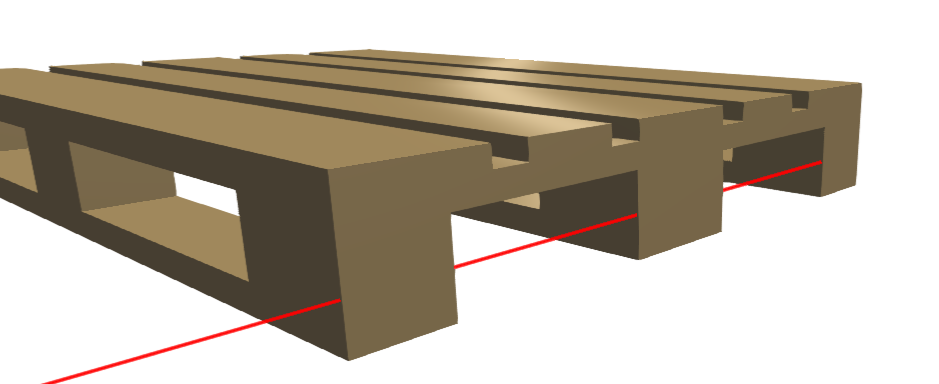
In the next picture, the right palette is approximated (simplified) with a (bounding) box which has the same outer dimension than the original object on the left side, only without the recesses.

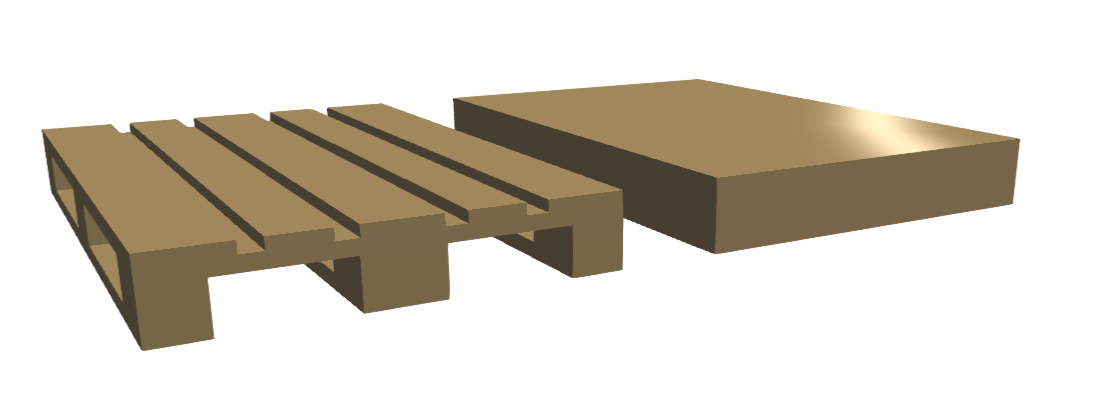
If you need to lift the pallets inside the recesses to separate them, the palette with the recesses need to be very accurately approximated.

Palette gets separated	Detail

Concave Vs Convex polygons

Basically, we decide between two different types of 3D model shapes:

Concave and Convex shapes.

The different between those two shapes is that a convex polygon does not have an inside dent in it's shape, whereas on a concave shape, one side of the shape is pointing towards the inside of the shape. To put this into real-life perspective, a concave shape curves inwards like an hourglass (or bowls or funnels), while a convex shape curves outwards like a football (think flatter surfaces and bumps).

Another concave shape can be found in pizza! Next time you have pizza, remove a slice of pizza!

Convex Pizza	Concave Pizza

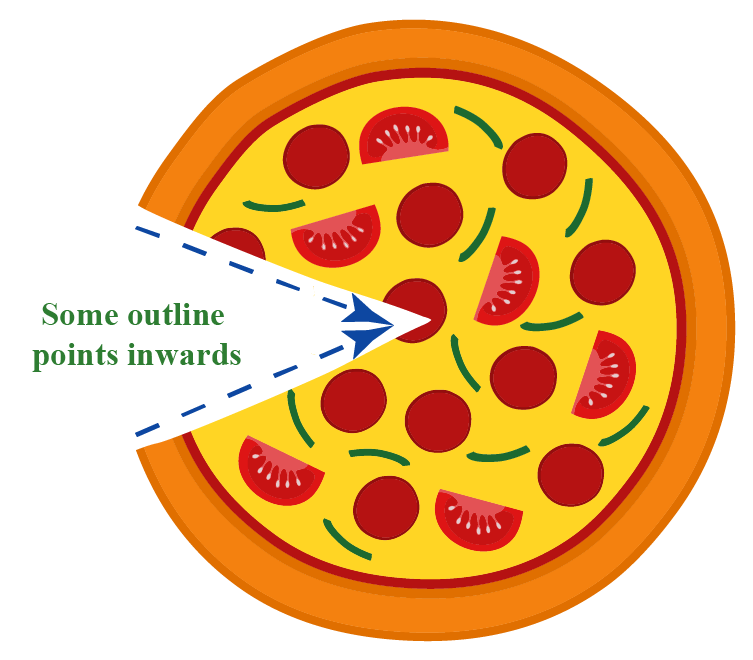Source: www.cuemath.com/geometry/convex-shapes-functions, called on December 20, 2022.

Note

Why do I need to know this? The problem: Calculating collisions of concave objects is computationally intensive. Therefore, we need to approximate concave polygons with convex ones.

We need convex polygons!

In order to ensure real-time interactivity during the collisions a first approach is to approximate the 3D models composing the scene by a set of simple convex shapes such as ellipsoids, capsules, boxes or convex-hulls.

But like described in the first part on the top, it is up to the level of detail you would like to achieve.

Note

Also simple approximations can be sufficient!

In the following two figures, a complex 3D model is compared with the simplified pendant. The result on the right-hand side looks similar but is different to the original object.

Original mesh	Convex hull

A second approach consists in computing an convex decomposition of a surface, which consists in partitioning it into a minimal set of convex sub-surfaces (sub-meshes) using convex decomposition algorithms.

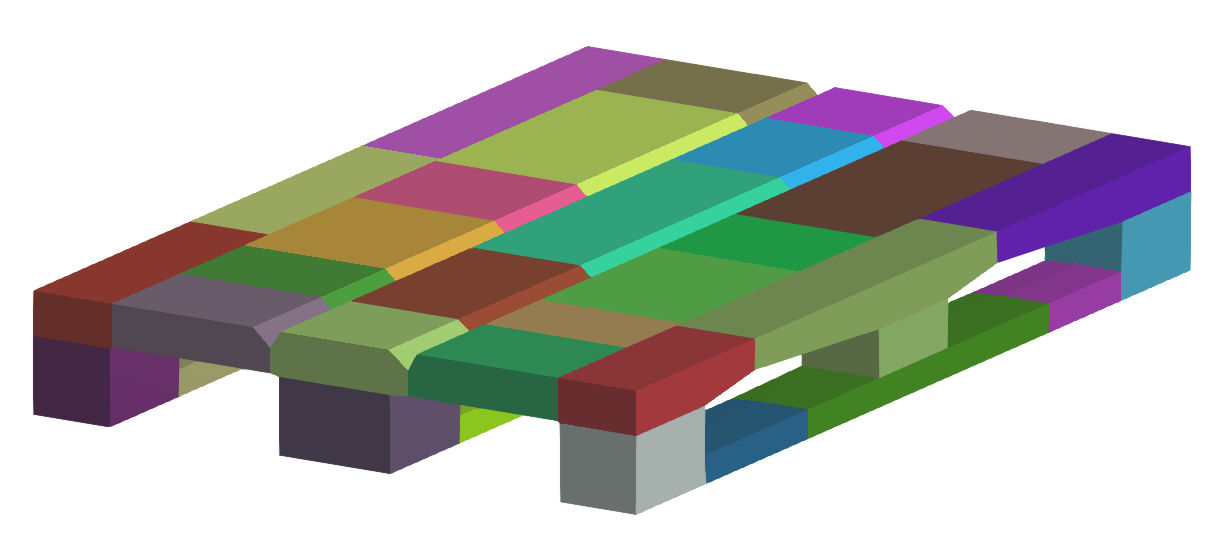
The result depends on the algorithm and on the parameters like the resolution (voxels). The higher the number of voxels, then the more fine details can captured.

This is shown in the following pictures. A high resolution leads to many sub-meshes and thus in most cases to the best result, but the computational effort for resolving collisions can be significantly higher.

Original Palette	7 Sub-Meshes	41 Sub-Meshes	2048 Sub-Meshes

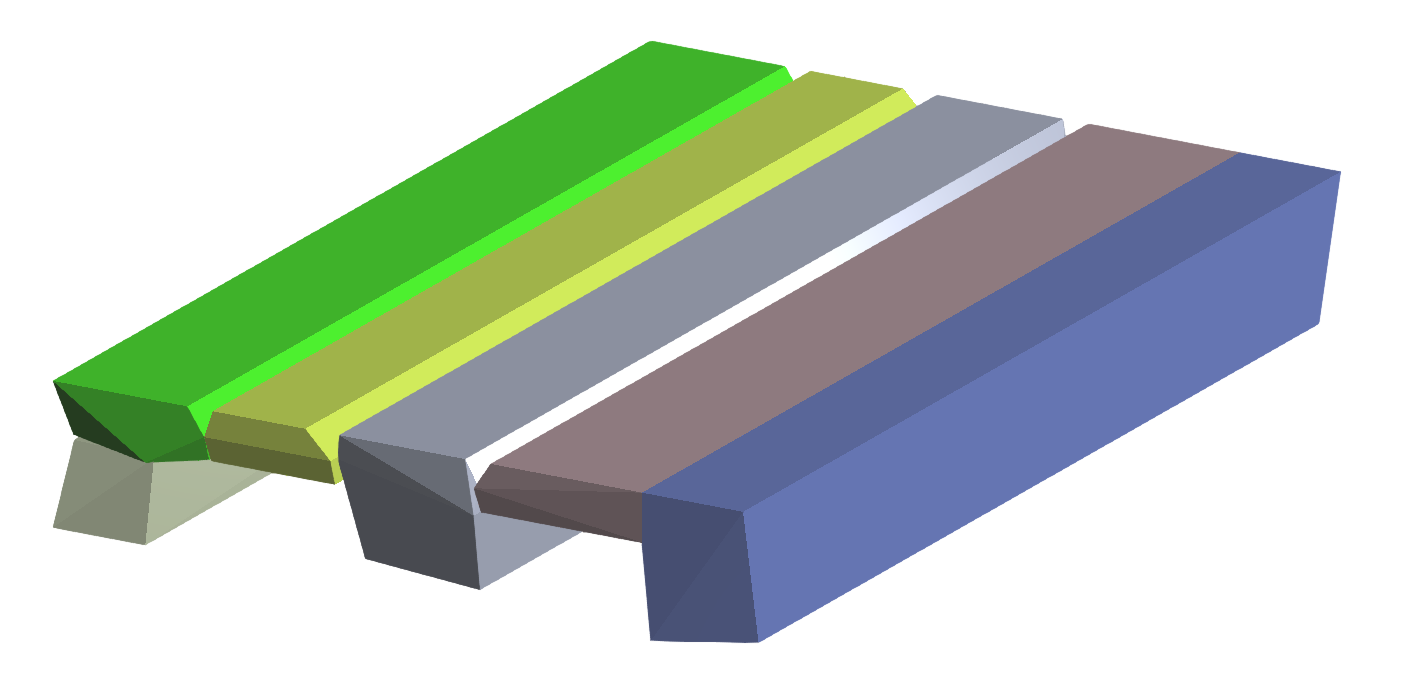To summarize: A process called convex decomposition is needed to convert a concave object into a convex one.

This and the other approximations are needed to ensure real-time interactivity during the collisions of the material with other materials and the environment.

Further Information

For more details visit the Video Guides section, where you can find additional information and video guides on this topic under Simulate complex 3D-Objects in real time.